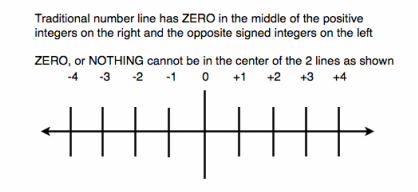
 Intro: You've seen this line a hundred million times, snaking its way along the roof line of your math class. Long, detailed fractions occassionaly interspersed with some positions for prime numbers. Enchanting color coordinated paper strips to complement the room's theme: MATHS (as some of the world calls it) Background: Having asked the following question many times and not receiving a sufficiently simple answer, I always wondered why teachers were so defensive when asked, "Since we are allowed to ask how parts of something are there in another something (allowed to divide any number by any other number) , "Why can't we divide any number by ZERO?" "Just because you can't - it's undefined!" was the retort. What did I know, I was a just an inquiriing student asking a question..... Let's digress for a minute. The concept of nothingness, emptiness, invisibility has been looked at by cultures in very different ways. If you can't see something it was relegated to the domain of the gods many years ago. Bacteria, electrons, magnetic fields, TV signals, practically the entire electromagnetic spectrum was invisible and unknown for most of human history. The very idea of having a symbol to represent NOTHINGNESS was tinkering with the realms of mystery and religion. Yet, as the world of maths evolved and we bumped into the need for a place marker to satisfy our position number system, voila the ZERO appeared. It was a brilliant solution. No longer was a Nine only a Nine. If it was to the left of a zero, it was Nine units of ten, and no units of ones, resulting in 90. We leapt from hash marks on endless streams of paper, crossing every fourth mark to make an easy counting by fives, it was obvious looking at an abacus that something was needed to represent a positional nothing. Slowly, this symbol, not really a number, began to have equality to a number. We recited and placed it in the lowest integer position. We were taught that any number multiplied by zero equaled zero. (At least they didn't teach us that it was undefined) I just wish they had insisted in our learning that multiplying by zero is a fantastic journey of imagination, stating the process a little differently: 3 times 2 would be stated "What is the total of 2 sets of 3?" Then when asked, 3 times 0 would turn out to be "What is the total of ZERO sets of 3? -- No need to make a didactic rule stating that all numbers multiplied by zero would be zero, the question doesn't even deserve an answer. 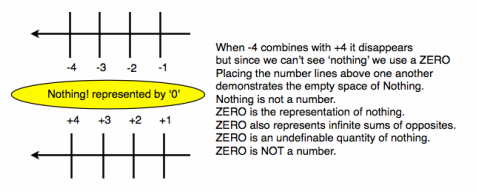 Freeing Zero from its Numerical Prison! So the next time you hear that you can't divide by ZERO, your answer may be, "Of course you can't, Zero is not a number!"
0 Comments
Leave a Reply. |
Archives
February 2020
AuthorSubscribe to Podcasts Only using iTunes or other RSS Feed program: Categories
All
|
Thinking about Things...
 RSS Feed
RSS Feed